Source BRION 1982, p.11
V.3.0.9 - Dernière mise à jour : 04/05/2015
Pour représenter les données quantitatives repérées (échelles d'intervalles), les ratios et pourcentages (échelles de rapport) et les données qualitatives exprimant la chronologie, la hiérarchie, ... (échelles ordinales).
Variable visuelle utilisée : la Valeur
Objectif : faire varier la valeur d'un figuré pour traduire l'ordre (hiérarchie relative) entre les objets
- En implantation ponctuelle
variation du "niveau de gris" à l'intérieur de surfaces de taille constante
- En implantation linéaire
variation du "niveau de gris" à l'intérieur de lignes de largeur constante
- En implantation surfacique (cas le plus simple)
variation du "niveau de gris" à l'intérieur des polygones
Synonyme : découper en classes, partitionner
Discrétiser c'est regrouper en classes, de manière pas trop arbitraire, des données quantitatives (sous certaines conditions qualitatives)
- Données quantitatives
- échelles :
- mesurées ou dénombrées ;
- repérées ;
- échelle :
- de rapport (les ratios et pourcentages).
On passe d'une variable continue a une variable discrète
- Données qualitatives
- On ne parle pas de discrétisation
- On peut évoquer un regroupement de modalités
Les données qualitatives identifiées par leur échelle ordinale sont déjà en classes
=> classes des grands ou des petits, etc.
- Que discrétise-t-on ?
une distribution
Colette CAUVIN considère qu'il y a 4 familles de distribution (cf. CAUVIN 1987, p.16)
- distributions normales (ou proche de la loi normale) où :
- le + grand nombre d'individus est dans les classes centrales
- ce nombre s'amenuise vers les pieds de courbes
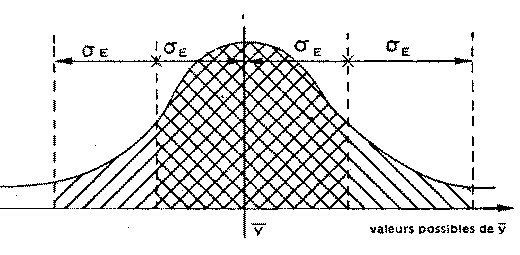
fig. 1 - Concentration des individus dans une distribution normale

- la répartition des individus est connue de part et d'autre de la moyenne*
quelque soit la valeur de l'écart-type*
, par exemple :
- 68,3 % des individus appartiennent à l'intervalle [
-
;
+
] ;
- 95,4 % des individus appartiennent à l'intervalle [
- 2 *
;
+ 2 *
] ;
- 99,7 % des individus appartiennent à l'intervalle [
- 3 *
;
+ 3 *
] ;
- etc.
(cf. CHADULE 1997, p.193, Annexe K)
La loi normale est bien connue. Elle sert de référentiel pour comparer les distributions, mais c'est un référentiel parmi d'autres.
Mais cette distribution est rare en géographie
- distributions asymétriques* (modérément ou non)
Synonyme : dissymétrique*
- concentration dans les petites ou grandes valeurs
- asymétrie par rapport aux valeurs centrales*
Exemple : nombre de salariés (Y) en fonction des revenus (X) !
=> asymétrie gauche
Indique que le phénomène augmente de façon multiplicative dans une direction, contrairement aux phénomènes additifs qui suivent une loi normale (accroissement additif). On ne peut normalement pas utiliser les paramètres usuels de discrétisation sur les distributions asymétriques.
Ce sont les distributions les plus fréquentes en géographie
- distributions uniformes
- quelque soit la valeur de l'abscisse X toutes les valeurs de l'ordonnée Y sont égales
- phénomènes discrets
fig. 4 - Distribution uniforme
Exemple : nombre d'élus (Y) en fonction de la population de la circonscription (X) !
Ce sont des distributions rares en géographie
- distributions plurimodales
- variables composées de sous populations + ou - imbriquées
fig. 5 - Distribution plurimodale
Les paramètres statistiques classiques sont sans signification
Il faut décomposer cette distribution en plusieurs distributions avant de l'étudier.
Donc avant de discrétiser :
On visualise la structure de la variable par son diagramme de distribution*
- Le diagramme de distribution* :
- n'a pas de signification mathématique
- permet de visualiser la forme de la distribution
L'axe des X doit être le plus détaillé possible
- A titre d'exemple, on peut prendre le vote écologiste aux élections régionales de 1998 (Paris + Seine-Saint-Denis)
fig. 6 - Diagramme de distribution
Un point représente une commune
- L'histogramme
A partir de ce diagramme, on peut tracer un histogramme
ou mieux :
- Une courbe des fréquences cumulées
fig. 8 - Courbe des fréquences cumulées
Donne une idée :
- de la fonction d'ajustement ;
- des limites de classes.
- Prendre l'exemple : Répartition de la surface boisée par département en France métropolitaine - (Sources : Inventaire forestion national - IFN).
Ce fichier est au format EXCEL ".xls" et "pèse" 97 Ko.
- prendre l'onglet Tab1b ;
- calculer les minimum, maximum, etc.
- calculer les matrices des fréquences ;
- calculer les fréquences relatives simples (en pourcentages) ;
- calculer les fréquences relatives cumulées (en pourcentages) ;
- tracer l'histogramme (le diagramme en bâtons dans EXCEL) des fréquences relatives cumulées (en pourcentages) sur la matrice (E3:E9) ;
- tracer la courbe des fréquences relatives cumulées (en pourcentages) sur la matrice (E13:E55).
- Quelle est la forme de la distribution ?
Il faut maintenant s'interroger sur le nombre optimal de classes d'une discrétisation.
- Il n'y a pas de règles universelles, que des solutions empiriques et pragmatiques.
Mais l'objectif est de :
1) conserver à la distribution sa forme générale
2) apporter le maximum d'information
- Il faut naviguer entre un :
- découpage trop fin (trop grand nombre de classes)
où l'effectif par classe risque d'être trop faible et sa répartition aléatoire (car fonction du découpage)
- découpage trop grossier (trop petit nombre de classes)
avec une perte d'information et une schématisation extrême
Que ce soit à des fins
cartographiques ou statistiques
- Pour constituer un découpage significatif, deux méthodes sont proposées :
qui tiennent compte de l'effectif* total de la distribution
elles sont décrites (entre autre) dans le CHADULE 1974 p.32
Pour Brooks-Carruthers, le nombre de classes K1 doit être :
K1 < 5 log10 M
avec M le nombre d'individus (nb. de départements de l'exemple)
Pour Huntsberger, le nombre de classes K2 doit être :
K2 = 1 + 3,3 log10 M
- Qu'en est-il pour les 95 départements de l'exemple ?
K1 < 5 log10 M < 5 log10 95 < 5 * 1,98 < 9,89
K2 = 1 + 3,3 log10 M = 1 + 3,3 log10 95 = 7,52
Un nombre de 8 classes semble pouvoir convenir.
- Reprendre l'exemple du tableau 1
- prendre l'onglet Tab1b ;
- vérifier le nombre de départements en C104 avec la fonction "nombre" (NB) ;
- calculer le nombre de classes avec les deux méthodes empiriques précédentes (en C106 et C107) ;
- Combien de classes retenez-vous ?
- 8 classes semble être un bon compromis !
Cela explique que :
- pour une amplitude de 626 450 (C102) ;
- et 8 classes ;
on ait un pas de 78 306,25 (E3:E10) efficace (pour montrer que la distribution n'est pas normale !).
- Toutefois, d'autres raisons peuvent guider le choix du nombre de classes :
- Des raisons techniques
la cartographie infographique ou "manuelle" est difficile au delà de 5 ou 7 paliers
le découpage à l'aide de la moyenne et de l'écart-type est cohérent en 5 ou 7 paliers
- Des raisons pratiques
un résumé de la distribution est parfois suffisant en 3 ou 4 classes
- Quelques indices sont proposés au chapitre 4 pour faciliter le choix du nombre de classes.
Il répond comme le nombre de classes à certaines conditions :
- Par convention des valeurs simples
retenir des paliers "ronds", "naturels"
- Une borne appartient à une classe et une seule
- La borne inférieure est incluse
- La borne supérieure est exclue
- Les bornes sont, de préférence :
- là où il y a des seuils*, des discontinuités*
- là où la variable a un faible effectif
- Certaines valeurs significatives comme :
- "zéro" pour le taux d'accroissement
- "2,1" pour l'indice de fécondité
- pour certains auteurs, la moyenne dans le cadre d'un distribution normale
Les quatre méthodes les plus courantes (utiles)
Synonyme : Discrétisation en classes d'égale fréquence
Repose sur une étude de la fréquence de la variable et non de ses valeurs
Caractérise des classes contenant un même nombre d'unités statistiques mais de taille variable
effectif égaux par classe K (à ± 1 près)
Mk = M / K
où
Mk est l'effectif par classe
M est le nombre d'unités statistiques
K est le nombre de classes
Permet de faire des groupes équilibrés mais :
- ignore les particularités de la distribution
- regroupe des individus très éloignés (par exemple les dix 1er, puis les dix suivants, etc.)
- d'amplitude inégale
Conseillées lorsque la distribution :
- n'offre pas de seuils nets ;
- est uniforme (mais également normale) ;
- contient des valeurs douteuses (!)
Peu sensibles aux valeurs exceptionnelles, car on considère les observations selon leur ordre et non selon leur valeur.
Cette méthode :
- Fait des classes équilibrées ;
- Apporte un maximum d'information (autant d'individus pour chaque classe).
- Prendre l'exemple : Surface des terrains forestiers domaniaux
- Téléchargement du tableau "cfm32ta2b.xls"
Ce fichier est au format .xls et "pèse" 97 Ko.
- prendre l'onglet Tab2b ;
- pour révision, refaire le calcul de la matrice intervalles
- prendre l'onglet Tab2c ;
- vérifier le nombre de départements en D99 ;
- calculer le nombre de classes avec les deux méthodes empiriques précédentes (en D102 et D103) ;
- Combien de classes retenez-vous ?
- toujours dans l'onglet Tab2c ;
- calculer le nombre de départements par classe en D107 ;
- après avoir trié les colonnes A, B, C et D sur les surfaces (colonne C), tracer en colonne E avec des plages de couleurs (de valeurs croissantes en théorie) les partitions ;
- inscrire les seuils retenus (comme en D16).
Synonyme : Discrétisations selon la moyenne et l'écart-type
Implique en principe une distribution normale (ou normalisée)
Les classes :
- ont en générale la même étendue, sauf (souvent) les extrêmes
- encadrent la moyenne
[minimum ;
- 2 *
[ ;
[
- 2 *
;
- 1 *
[ ;
[
- 1 *
;
[ ;
[
;
+ 1 *
[ ;
[
+ 1 *
;
+ 2 *
[
etc.
- ou englobent la moyenne
[minimum ;
- 1,5 *
[ ;
[
- 1,5 *
;
- 0,5 *
[ ;
[
- 0,5 *
;
+ 0,5 *
[ ;
[
+ 0,5 *
;
+ 1,5 *
[ ;
etc.
Préférable d'englober la moyenne, car on regroupe les valeurs peu significativement différentes de 0 dans la même classe.
- sont au nombre de :
- 3, 5 ou 7 quand elles englobent ;
- 4, 6 ou 8 quand elles encadrent ;
- Conseillées :
- pour leur valeur probabiliste
Par exemple :
- 68,3 % des individus appartiennent à l'intervalle [
-
;
+
] (cf. supra)
- pour des comparaisons indépendantes des valeurs de la variables
lorsqu'on exprime les paliers par rapport à la moyenne et l'écart-type.
Mais alors, la double légende s'impose !!!
- Déconseillées lorsque :
- les distributions sont dissymétriques (et non transformées, cf. Chapitre 3.);
- il y a des valeurs exceptionnelles (influence sur les calculs de la moyenne et de l'écart-type).
- Reprendre l'exemple : Surface des terrains forestiers domaniaux
- reprendre l'onglet Tab2c ;
- calculer la moyenne et l'écart-type en F109 et F110 ;
- calculer pour 7 classes les seuils :
- 2,5 *
(en F112) ;
- 1,5 *
(en F113) ;
- 0,5 *
(en F114) ;
etc.
- tracer en colonne F avec des plages de couleurs (de valeurs croissantes en théorie) les partitions ;
- inscrire les seuils calculés.
Implique que la moyenne est une "valeur" qui sépare deux ensembles.
Quelle traduit un point d'équilibre dans la distribution.
C'est une démarche itérative.
- 1ère étape :
- calcul de la moyenne de premier ordre moy1 sur l'ensemble de la distribution
- partition en deux sous ensembles
- [minimum ; moy1[
- [moy1 ; Maximum]
- 2e étape :
- calcul des moyennes de deuxième ordre moy2a et moy2b sur chaque sous partie
- partition en quatre sous ensembles
- [minimum ; moy2a[
- [moy2a ; moy1[
- [moy1 ; moy2b[
- [moy2b ; Maximum]
- 3e étape :
- calcul des moyennes de troisième ordre moy3a , moy3b , moy3c et moy2d sur chaque sous partie
- partition en huit sous ensembles
On peut réitérer l'opération indéfiniment.
- Avantages :
- fréquences également réparties dans les classes ;
- étendues des classes assez proches avec :
- intervalles assez étroits dans les zones modales ;
- intervalles assez lâches dans les secteurs de faible fréquence.
- pour une distribution asymétrique gauche
donne des classes comparables à une discrétisation par progression géométrique
- Inconvénients :
- nombre de classes :
- imposé ;
- qui croît par puissance de deux et pas arithmétiquement.
- l'ajout d'un individu impose un recalcul complet ;
- impossibilité de faire une classe moyenne (!) ;
- oppose des valeurs de part et d'autre des moyennes (alors qu'elles peuvent être proches !).
Il existe d'autres discrétisations statistiques (ou probabilistes) comme :
- la méthode de Jenks (fondée sur la notion de variance) ;
- discrétisation en classes équiprobables [construction des classes par rapport à une distribution théorique (comme la loi normale)] ;
- etc.
- Reprendre l'exemple : Surface des terrains forestiers domaniaux.
- prendre l'onglet Tab2c ;
- calculer les moyennes de deuxième ordre moy2a et moy2b (en G122 et G123) ;
- calculer les moyennes de troisième ordre moy3a, moy3b, moy3c et moy3d (de G126 à G129) ;
- tracer en colonne G avec des plages de couleurs (de valeurs croissantes en théorie) les partitions ;
- inscrire les seuils calculés.
Synonyme : Classes d'égale étendue*
- La progression est à intervalles constants
Caractérise des classes de pas constant contenant un nombre d'unités statistiques variables
e = (Y
max - Y
min) / K
où
e est l'étendue de chaque classe ;
Y
max est la valeur maximale de l'effectif ;
Y
min est la valeur minimale de l'effectif ;
K est le nombre de classes.
- La 1ère classe vaut [ Y
min ; Y
min + e[
qui se lit : va de Y
min inclus à Y
min + e exclu
- La 2e classe vaut [ Y
min + e ; Y
min + 2e[
etc. jusqu'à Ke classe
- La Ke classe vaut [ Y
min + (K - 1) * e ; Y
min + K * e]
avec
Y
min + K * e = Y
max
- Permet de faire des paliers "ronds"
mais
- si la distribution est discontinue => risque de classes vides ;
- si la distribution est asymétrique => effet de masse en début ou fin de distribution ;
- si la distribution est normale => effet de masse au centre de la distribution.
Conseillées lorsque :
- la distribution est relativement uniforme* ou normale
- le min et le max sont significatifs
- Reprendre l'exemple : Surface des terrains forestiers domaniaux.
- prendre l'onglet Tab2c ;
- calculer l'étendue (en H133) ;
- pour 8 classes les seuils :
min + e (en H135) ;
min + 2e (en H136) ;
min + 3e (en H137) ;
etc.
- tracer en colonne H avec des plages de couleurs (de valeurs croissantes en théorie) les partitions ;
- inscrire les seuils calculés.
- La progression est arithmétique, logarithmique ou géométrique
Discrétisation à utiliser sur des séries asymétriques à gauche pour détailler les petites valeurs
Plus complexe à mettre en oeuvre et surtout à expliquer au lecteur
Préférer les moyennes emboîtées par exemple ou les transformations
- Méthode des seuils naturels
Synonyme : Discrétisation selon les seuils observés (ou naturels)
On repère sur :
- le diagramme de distribution ou l'histogramme des fréquences
les minimum
- la courbe des fréquences cumulées
les paliers
Elle est parfois simple à réaliser, c'est un "découpage naturel"
mais
- souvent difficile à justifier
- n'est pas très scientifique (reproductibilité aléatoire !)
Elle est parfois utilisée pour finaliser les précédentes :
- recherche de paliers "ronds" ;
- légères translations des limites vers les vides de la distribution ;
- etc.
C'est la seule qui fonctionne sur les distributions plurimodales*.
- Faire une transformation c'est :
- utiliser 1 fonction de la variable au lieu de la variable elle-même
- faire un changement d'échelle
- on passe d'une échelle originelle à une autre ;
- on convertit l'intervalle entre les données.
- L'effet global est de modifier la forme de la distribution des fréquences
Ainsi une variable dissymétrique à gauche est :
- symétrisée ;
- normalisée (même).
par une transformation logarithmique
- La transformation logarithmique permet :
- d'augmenter l'intervalle entre les faibles valeurs ;
- d'atténuer leur concentration en les écartant de l'origine ;
et surtout,
- d'y appliquer les statistiques paramétriques.
Pour en savoir plus sur les logarithmes, cliquez ici !
fig. 8b - Effet des transformations
- Quels sont les partis qui ont une asymétrie droite, gauche ?
fig. 9 - Le pourcentage des voix aux élections régionales de 1998 par commune (dép. 75 et 93)
Sources : Le Monde du 18 mars 1998 et Le Parisien du 16 mars 1998Pour la construction du diagramme en boîtes et moustaches voir la fiche mémo fm24sta.htm du cours de statistique
Un des cas les plus courant en géographie
fig. 10 - Le pourcentage des voix de la Droite aux élections régionales de 1998 par commune (dép. 75 et 93)
Sources : Le Monde du 18 mars 1998 et Le Parisien du 16 mars 1998
On normalise une variable de ce type par :
- une fonction puissance
où l'exposant est inférieur à 1 (racine carré, cubique , ...)
quand la dissymétrie gauche est faible (exposant 1/2 dans EXCEL)
- une fonction logarithmique
très usuelle
quand la dissymétrie gauche est plus forte (Log10 dans EXCEL)
- Reprendre l'exemple du tableau 1
- prendre l'onglet Tab1c ;
- compléter les colonnes D et E ;
- compléter les tableaux de fréquences des colonnes G à J ;
- faire 1 histogramme par tableau de fréquences (sur les pourcentages non cumulés) ;
- Quelle est la transformation la plus efficace (celle qui rapproche le plus la distribution de la loi normale) ?
- Nécessité de calculer les coefficients d'asymétrie* et d'aplatissement*
Ils caractérisent tous les deux la forme de la distribution.
Ils se calculent à l'aide des moments centrés*.
- Un moment
centré ( ![]() ; se lit mu)
d'ordre r est
:
; se lit mu)
d'ordre r est
:
la moyenne arithmétique des écarts à la moyenne arithmétique élevé à la puissance r :
formule n°1 (mem32car.htm)
- La variance, notée (![]() ; se lit sigma deux) et, déjà vue en statistique, est :
; se lit sigma deux) et, déjà vue en statistique, est :
- un moment centré d'ordre 2 ;
- la moyenne arithmétique des carrés des écarts à la moyenne.
formule n°3 (mem41sta.htm)
- Le Coefficient d'asymétrie de Fisher,
noté (![]() ; se
lit gamma un), est le quotient suivant :
; se
lit gamma un), est le quotient suivant :
formule n°2 (mem32car.htm)
avec :
-
le moment centré d'ordre 3 ;
-
l'écart-type élevé au cube.
Donc, il peut être négatif !
- Quand :
Coef. d'asymétrie < 0 => asymétrie gauche
Coef. d'asymétrie = 0 => distribution normale
Coef. d'asymétrie > 0 => asymétrie droite
- Dans EXCEL, la formule est la suivante :
formule n°3 (mem32car.htm)
où :
m est l'effectif d'un échantillon ;
s est l'écart-type calculé sur un échantillon.
Elle s'appelle : COEFFICIENT.ASYMETRIE
Synonyme => Skewness
- Reprendre l'exemple du tableau 1
- prendre l'onglet Tab1c ;
- calculer les coefficients d'asymétrie (de C107 à E107) ;
- Quelle est la transformation la plus efficace (celle qui rapproche le plus la distribution de la loi normale) ?
- Quel est le signe du coefficient ?
L'asymétrie n'est pas tout,
il faut également évaluer l'aplatissement
- Le Coefficient d'aplatissement de Pearson,
noté (![]() ; se
lit bêta deux), est le quotient suivant
:
; se
lit bêta deux), est le quotient suivant
:
formule n°4 (mem32car.htm)
avec :
-
le moment centré d'ordre 4 ;
-
le carré de la variance.
Donc, il est toujours positif !
- Quand :
Coef. d'aplatissement = 3
Il est le même que celui d'une courbe gaussienne.
- Reprendre l'exemple du tableau 1
- prendre l'onglet Tab1c ;
- calculer les coefficients d'aplatissement (de C108 à E108) ;
Mais, ce coefficient est absent d'EXCEL, il faut le calculer :
- calculer les écarts à la moyenne en colonnes L, M et N ;
- ils complètent le quotient qui donne le coef. d'aplatissement
- Quelle est la transformation la plus efficace (celle qui rapproche le plus la distribution de la loi normale) ?
Si vous n'arrivez pas à vous décider sur la transformation la plus efficace :
- calculer le rapport (de C109 à E109).
Il existe dans EXCEL une fonction équivalente qui s'appelle : KURTOSIS
- Allez la voir dans la rubrique d'aide d'EXCEL
- Quand :
Kurtosis < 0 => distribution aplatie
Kurtosis = 0 => distribution "normale"
Kurtosis > 0 => distribution pointue
- Reprendre l'exemple du tableau 1
- prendre l'onglet Tab1c (2) cette fois-ci ;
- calculer les coefficients (de C102 à F114) ;
- colorier selon le code couleur fourni.
- Quelle est la transformation la plus efficace (celle qui rapproche le plus la distribution de la loi normale) ?
Si vous n'arrivez pas à vous décider sur la transformation la plus efficace :
- calculer les écarts de la ligne 115.
En conclusion, la transformation n'est pas parfaite
mais il faut faire un choix !
Un exemple, malgré tout, moins courant en géographie que l'asymétrie gauche
fig. 11 - Le pourcentage des voix de la Gauche plurielle aux élections régionales de 1998 par commune (dép. 75 et 93)
Sources : Le Monde du 18 mars 1998 et Le Parisien du 16 mars 1998
On normalise une variable de ce type par :
- une fonction puissance
où l'exposant est supérieur à 1 (puissance deux, trois, ...)
quand la dissymétrie droite est faible (exposant 2 dans EXCEL)
- Reprendre l'exemple du tableau 1
- prendre l'onglet Tab1d ;
- refaire les calculs (comme au paragraphe 3.1.1.)
- A moins de déceler une répétitivité, peu de discrétisations sont satisfaisantes sur les distributions plurimodales (Cf. fig. 12)
fig. 12 - Le pourcentage des voix du Front national aux élections régionales de 1998 par commune (dép. 75 et 93)
Sources : Le Monde du 18 mars 1998 et Le Parisien du 16 mars 1998
- Le diagramme en boîtes et moustaches (fig. 9) permettait-il de voir la bimodalité de la distribution ?
Plus par habitude que par nécessité (cf. CAUVIN 1987, p.53),
les discrétisations sur données transformées se font surtout par les méthodes des :
- classes d'égales étendues ;
- moyennes et écart-types
Mais toutes les autres sont valables.
Des aides à la décision
Objectif : sélectionner la discrétisation la plus fidèle aux données d'origine
Car discrétiser une distribution c'est commettre une erreur
On va limiter celle-ci par
comparaison des valeurs initiales et des valeurs représentées sur la carte
à l'aide d'indices
Deux indices sont proposés ici :
- Le TAI (Tabular Acuracy Index) de Jenks ;
- L'analyse des variances intra et inter-classes.
Compare l'écart, en valeur absolue, entre les individus et la moyenne de leur classe et ces mêmes individus et la moyenne générale , toujours en valeur absolue.
formule n°5 (mem32car.htm)
avec :
- h le nombre de classes variant de 1 à k ;
écart à la moyenne, en valeur absolue, dans la classe h ;
écart à la moyenne générale, en valeur absolue ;
où :
-
moyenne de la classe h ;
-
moyenne générale ;
-
un individu
de la classe h ;
- M effectif de la série ;
- Mh effectif de la classe h.
Le TAI varie entre 0 et 1
- Quand :
- le TAI ± 1 => la somme des écarts intra-classes est plus faible que la somme des écarts à la moyenne générale
la discrétisation crée des classes homogènes
- le TAI ± 0 => la somme des écarts intra-classes est peu différente de la somme des écarts à la moyenne générale
la discrétisation crée des classes peu homogènes
- Reprendre l'exemple : Analyse du PIB par habitant des régions de France, d'Italie et d'Espagne en 1991 - (Sources : Eurostat, 1992, in SAINT-JULIEN 1999, p.23).
- prendre l'onglet Tab2d ;
- recopier les couleurs matérialisant les classes du Tab2c vers le Tab2d ;
- calculer en E6 l'écart absolu à la moyenne de la valeur du 1er PIB de la 1ère classe à l'aide la formule suivante :
=ABS(D6-MOYENNE(D$6:D$??))
- remplacer les deux "??" par le n° de ligne qui contient la dernière cellule de cette première classe ;
- recopier vers le bas sur toute la 1ère classe.
- faire la même manip pour l'ensemble des classes ;
puis pour les trois autres discrétisations.
- calculer la somme des écarts à la moyenne, pour les 6 à 8 classes de chaque discrétisation (de E72 à H79) ;
puis faire la somme de ces écarts par discrétisation (de E86 à H86) ;
- calculer la somme des écarts à la moyenne générale (de I6 à I63) ;
puis faire la somme des écarts à la moyenne générale (en I84)
- enfin, calculer le TAI (de E86 à H86).
- Quelle est la méthode qui donne les classes les plus homogènes ?
Là encore, il s'agit de déterminer si les individus d'une classe se ressemblent plus qu'ils ne ressemblent à ceux d'une autre classe.
La variance totale (notée![]() ), ou encore
information totale, se décompose en :
), ou encore
information totale, se décompose en :
Variance totale = Variance inter-classes + variance intra-classes
formule n°6 (mem32car.htm)
avec :
variance inter-classes ;
variance intra-classes ;
où :
-
moyenne de la classe h ;
-
moyenne générale ;
-
un individu
de la classe h ;
- M effectif de la série ;
- Mh effectif de la classe h.
L'indice I se calcule comme suit :
I = (Variance intra-classes / Variance inter-classes)
L'indice I varie entre 0 et 1
- Quand :
- I ± 1 => plus la variance intra est forte par rapport à la variance inter
plus la discrétisation crée des classes hétérogènes
- I ± 0 => plus la variance intra est faible par rapport à la variance inter
plus la discrétisation crée des classes homogènes
Attention, la lecture est donc inversée par rapport au TAI
- Reprendre l'exemple : Analyse du PIB par habitant des régions de France, d'Italie et d'Espagne en 1991 - (Sources : Eurostat, 1992, in SAINT-JULIEN 1999, p.23).
- prendre l'onglet Tab2e ;
- recopier les couleurs matérialisant les classes du Tab2c vers le Tab2e ;
- calculer en E6 l'écart à la moyenne de la valeur du 1er PIB de la 1ère classe à l'aide la formule suivante :
=(NB(D$6:D$??)/(NB(D$6:D$63))^2)*(D6-MOYENNE(D$6:D$??))^2
- remplacer les deux "??" par le n° de ligne qui contient la dernière cellule de cette première classe ;
- recopier vers le bas sur toute la 1ère classe.
- faire la même manip pour l'ensemble des classes ;
puis pour les trois autres discrétisations.
- calculer la somme des écarts à la moyenne au carré (la variance intra), pour les 6 à 8 classes de chaque discrétisation (de E84 à H84) ;
- calculer en E72 l'écart à la moyenne de la valeur du 1er PIB de la 1ère classe à l'aide la formule suivante :
=(NB(D6:D??)/NB(D6:D$63))^2*((MOYENNE(D6:D??)-(Tab2c!F$77))^2)
- remplacer les deux "??" par le n° de ligne qui contient la dernière cellule de cette première classe.
- faire la même manip pour l'ensemble des classes ;
puis pour les trois autres discrétisations.
- enfin, calculer l'indice I (de E87 à H87).
- Quelle est la méthode qui donne les classes les plus homogènes ?
- Est-ce les même résultats que pour les TAI ?
- Comment représenter cartographiquement le pourcentage des voix obtenues lors des élections régionales de 1998 ?
- Téléchargement de la base de données cartographiques
Nécessite le téléchargement de 2 fichiers Géoconcept
Il semblerait que le téléchargement de la base de données cartographiques soit de mauvaise qualité avec Netscape (au moins la V4.5). Il est donc recommandé d'utiliser Internet Explorer comme navigateur pour télécharger ce travail.
fichier n°1 - Téléchargement du fichier "cfm32ca1.gcm"
Ce fichier est au format Géoconcept et "pèse" 27 Ko.
fichier n°2 - Téléchargement du fichier "cfm32ca1.gcr"
Ce fichier est au format Géoconcept et "pèse" 596 Ko.
- Téléchargement du Tableau 1 - Résultats des élections régionales (en % des suffrages exprimés) à Paris et en Seine-Saint-Denis en 1998 par commune - (Sources : Le Monde du 18 mars 1998 et Le Parisien du 16 mars 1998).
Téléchargement du tableau "cfm32ta1.xls"
Ce fichier est au format EXCEL ".xls" et "pèse" 97 Ko.
- Quel est le champ commun entre la base Géoconcept et le fichier texte (l'ouvrir dans EXCEL) ?
C'est lui qui va servir de clef d'importation (jointure*)
- À quels Type et Sous-type est-il attaché ?
- Le fichier "cfm32ta1.xls" n'est pas prêt à l'importation dans Géoconcept.
- Il faut faire un onglet avec les données qui vous intéressent ;
- Le convertir en un fichier texte ".txt"
qui comporte deux champs qui peuvent servir de jointure :
- Nom
- Code Commune
N'importe lequel de ces champs peut servir de champ clef.
- Les autres champs concernent les résultats des élections :
- RPR-UDF => Union de l'opposition ;
- Gauche plurielle => PCF, PS, les Verts, MDC et PRG ;
- FN => Extrême droite ;
- Extr. gauche => LO, LCR, ... ;
- Écologistes => GE, ... ;
- Divers droites => ... ;
- Divers => CNPT, Parti humaniste, ...
Ouvrir la carte "cfm32ca1.gcm", puis :
- Menu Fichier
- Sous menu Importer/Mettre à jour ...
- Choix du fichier texte
en Type : ASCII texte délimité
puis Ouvrir
- Créer une configuration temporaire
- Séparateur : Tab.
- Cocher : Noms des champs sur la première ligne
puis Suivant>
- Objets inexistants dans Géoconcept
- Ne pas cocher : Autoriser la création d'objets
- Objets inexistants dans le fichier d'import
- Laissez coché : Mettre dans une liste d'objet Géoconcept
puis Suivant>
- Type/Sous-type associé
- Laissez coché : Existant
- Menu déroulant : Commune (type valable pour tous les sous types)
Si l'on n'a pas créé précédemment les champs dans le configurateur
- maintenir sélectionnée chaque tête de colonnes qui contient aucun
- lui affecter le bon intitulé
- Laissez coché : Correspondance automatique entre champs du même nom
- Laissez coché : Création automatique des champs inexistants
puis Importer
Un message vous indique comment cela c'est passé.
Il doit y avoir 60 objets modifiés.
Vérifier dans la liste des objets, Menu Boite à outils, ces objets.
- Modifier dans le configurateur, Onglet Champs, le Genre des champs :
- RPR-UDF => Réels ;
- Gauche plurielle => Réels ;
- FN => Réels ;
- Extr. gauche => Réels ;
- Écologistes => Réels ;
- Divers droites => Réels ;
- Divers => Réels ;
Cartographie à l'échelle du 1/150 000
- Vérifier que les départements sont visibles à cette échelle (cf. Configurateur)
- Représentation par couche virtuelle
Menu Apparence
Sous menu Thématique ...
- Icône Plages de couleurs
- Aux objets : Commune
Donnez un nom à la couche virtuelle associée :
La 1ère carte porte sur le vote d'extrême gauche en classes d'égale amplitude en 7 classes => EG_CEA7
Soyez le plus fidèle possible à la thématique.
puis OK
- Champ Extr. gauche :
- Cocher : Classe de même largeur
- Nombre de classes : 7
- Ne pas modifier les apparences
- Cliquer sur OK
- Les paliers sont-ils facilement mémorisables ?
- Pour modifier la valeur de chaque palier :
- Le sélectionner dans la fenêtre Thématique
- Le modifier dans la fenêtre Classe
dans la case de saisie Min ou Max
- Cliquer sur OK
- La carte est-elle efficace ?
- Comment réduire cette impression d'opposition Paris/Banlieue ?
- Faire un essai avec une autre méthode de discrétisation
La 2e carte porte sur le vote d'extrême gauche en classes d'égale fréquence en 7 classes => EG_CEF7
- Quelles différences constatez-vous ?
- Laquelle sert quels buts ?
- Peut-on utiliser une autre méthode de discrétisation ?
- Si oui, laquelle ?
- Reprendre les transformations décrites aux paragraphes 3.1.1. et 3.1.2.
- Les cartographier pour les comparer
en conservant une légende commune
La légende doit :
- être retransformée en pourcentages pour l'édition des caissons de légende uniquement ;
- aller
- du minimum
- au maximum de toutes les distributions
- Quelle méthode de partition paraît la plus efficace ?
Reprendre l'exemple traité en statistique (mem32sta.htm et mem41sta.htm)
- On recherchera pour ces 3 pays la discrétisation du PIB par habitant la plus pertinente en se demandant : :
- Quel est le meilleur nombre de classes (pour quel public) ?
- Quelle est la meilleure méthode ?
Nécessite le téléchargement de 4 fichiers dont 2 fichiers Géoconcept
Il semblerait que le téléchargement de la base de données cartographiques soit de mauvaise qualité avec Netscape (au moins la V4.5). Il est donc recommandé d'utiliser Internet Explorer comme navigateur pour télécharger ce travail.
- Téléchargement de la base de données cartographiques
fichier n°1 - Téléchargement du fichier "cfm32ca2.gcm"
Ce fichier est au format Géoconcept et "pèse" 27 Ko.
fichier n°2 - Téléchargement du fichier "cfm32ca2.gcr"
Ce fichier est au format Géoconcept et "pèse" 59 Ko.
- Téléchargement du fond de carte renseigné
fichier n°3 - Téléchargement du fond de carte
(Sources : Code et localisation des régions de France, d'Italie et d'Espagne, in : SAINT-JULIEN 1999, p.25).
Ce fichier est au format ".TIF" et "pèse" 290 Ko.
- Téléchargement du Tableau 2 - PIB par habitant des régions de France, d'Italie et d'Espagne en 1991 - (Sources : Eurostat, 1992, in SAINT-JULIEN 1999, p.23).
fichier n°4 - Téléchargement du tableau "cfm32ta2.xls"
Ce fichier est au format .xls et "pèse" 97 Ko.
- Quel est le champ commun entre la base Géoconcept et le fichier texte (l'ouvrir dans EXCEL) ?
C'est lui qui va servir de clef d'importation (jointure*)
- À quels Type et Sous-type est-il attaché ?
- Reprendre les méthodes de partition décrites à la section 2.6.
- Les cartographier pour les comparer
en conservant leur légende propre
- Quelle méthode de partition paraît la plus efficace ?
- Est-ce celle désignée par les indices du chapitre 4 ?
Conclusion :
- pour comparer des distributions, par exemple :
- le même lieu à des dates différentes (progression d'un parti politique sur les mêmes bureaux de vote, ...) ;
- des lieux différents avec une légende commune, ...
- Quelles méthodes de partitions choisir ?
C'est encore un problème de forme des distributions
- Lorsqu'il y a comparaison de distributions (dans l'espace, le temps)
le découpage doit :
- être commun aux distributions (il sera donc arbitraire) ;
- présenter le même nombre de classes
- le plus robuste* possible
fig. 13 - Les deux cartes sont-elles comparables ?
Sources : Le Monde du 10 décembre 2005 in l'efficacité des ZEP en question, Martine Larouche
- la méthode des seuils naturels est à exclure, car elle :
- respecte chaque distribution ;
- ne suit pas de principe commun ;
- ne fournit pas systématiquement le même nombre de classes, ...
- la méthode de l'égale amplitude n'est valable, que lorsque les distributions :
- sont homogènes ;
- ne comportent pas de valeurs trop exceptionnelles ;
ou lorsque l'on doit faire une comparaison par rapport :
- à des cartes déjà réalisées ;
- à l'aide d'un découpage conventionnel (extérieur aux données).
- la méthode selon la moyenne et l'écart-type n'est valable, que lorsque les distributions :
- sont symétriques (ou transformées pour les rendre symétriques) ;
- ne comportent pas de valeurs trop exceptionnelles.
- la méthode de l'égale fréquence est la plus robuste
car elle tient compte de l'ordre des observations et pas des valeurs.
Elle est conseillée lorsque les distributions :
- sont de formes différentes (dissymétriques) ;
- contiennent des valeurs exceptionnelles (voire douteuses !) ;
- lorsque l'on ne veut pas effectuer de transformations de la variable.
Communiquez-moi sur la plateforme Moodle, à la rubrique travaux, les réponses aux questions suivantes :
Question n°3.2.1. Dans le cas d'une distribution ayant une forte asymétrie gauche, il est préférable d'utiliser une discrétisation par :
a) seuils naturels
d) moyennes emboîtées
b) standardisation
e) égale amplitude
c) égale fréquence
f) égal effectif
Question n°3.2.2. Dans le cas d'une distribution ayant une forte asymétrie gauche, il est préférable d'effectuer une transformation par :
a) la fonction puissance un demi
d) la fonction puissance deux
b) la fonction puissance un tiers
e) la fonction puissance trois
c) le logarithme
f) le trois quart centre
Question n°3.2.3. On réservera la discrétisation par la méthode de la moyenne et de l'écart-type pour les distributions :
a) avec une asymétrie droite
d) pluri-modales
b) avec une asymétrie gauche
e) en cloche
c) bi-modales
f) uniformes
NB : les mots suivis de "*" font partie du vocabulaire géographique, donc leur définition doit être connue. Faites-vous un glossaire.